lavaan package
![[http]](/moniwiki/imgs/http.png) tutorial(http://lavaan.ugent.be/tutorial/index.html)
tutorial(http://lavaan.ugent.be/tutorial/index.html)мқ„ л”°лқјн•ҙ ліёкұ°лӢӨ. lavaanлҠ” "latent variable analysis(мһ мһ¬ ліҖмҲҳ 분м„қ)"мқҳ м•ҪмһҗлӢӨ. мһ мһ¬ ліҖмҲҳлһҖ, кҙҖмёЎ ліҖмҲҳлЎңл¶Җн„° м¶”м •лҗҳм–ҙ진 추мғҒм Ғ к°ңл…җмқҳ ліҖмҲҳлҘј л§җн•ңлӢӨ. кө¬мЎ° л°©м •мӢқмқҳ ліҖмҲҳл“Өм—җ лҢҖн•ң м„ӨлӘ…мқҖ
![[http]](/moniwiki/imgs/http.png) м—¬кё°(http://blog.naver.com/lucifer246?Redirect=Log&logNo=173521493)
м—¬кё°(http://blog.naver.com/lucifer246?Redirect=Log&logNo=173521493)лҘј м°ёкі н•ҳмһҗ.
2 нҷ•мқём Ғ мҡ”мқё 분м„қ(cfa, confirmatory factor analysis) #
HolzingerSwineford1939 лҚ°мқҙн„°лЎң н•ҳлҠ”лҚ°, мқҙ лҚ°мқҙн„°м—җ лҢҖн•ң м„ӨлӘ…мқҖ
![[http]](/moniwiki/imgs/http.png) м—¬кё°(http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/lavaan/html/HolzingerSwineford1939.html)
м—¬кё°(http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/lavaan/html/HolzingerSwineford1939.html)лҘј м°ёкі н•ҳл©ҙ лҗңлӢӨ.
library("lavaan")
data(HolzingerSwineford1939)
str(HolzingerSwineford1939)
> library("lavaan")
> data(HolzingerSwineford1939)
> str(HolzingerSwineford1939)
'data.frame': 301 obs. of 15 variables:
$ id : int 1 2 3 4 5 6 7 8 9 11 ...
$ sex : int 1 2 2 1 2 2 1 2 2 2 ...
$ ageyr : int 13 13 13 13 12 14 12 12 13 12 ...
$ agemo : int 1 7 1 2 2 1 1 2 0 5 ...
$ school: Factor w/ 2 levels "Grant-White",..: 2 2 2 2 2 2 2 2 2 2 ...
$ grade : int 7 7 7 7 7 7 7 7 7 7 ...
$ x1 : num 3.33 5.33 4.5 5.33 4.83 ...
$ x2 : num 7.75 5.25 5.25 7.75 4.75 5 6 6.25 5.75 5.25 ...
$ x3 : num 0.375 2.125 1.875 3 0.875 ...
$ x4 : num 2.33 1.67 1 2.67 2.67 ...
$ x5 : num 5.75 3 1.75 4.5 4 3 6 4.25 5.75 5 ...
$ x6 : num 1.286 1.286 0.429 2.429 2.571 ...
$ x7 : num 3.39 3.78 3.26 3 3.7 ...
$ x8 : num 5.75 6.25 3.9 5.3 6.3 6.65 6.2 5.15 4.65 4.55 ...
$ x9 : num 6.36 7.92 4.42 4.86 5.92 ...
>
model <- "
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
"
fit <- cfa(model, data = HolzingerSwineford1939)
summary(fit, fit.measures = TRUE)
> summary(fit, fit.measures = TRUE)
lavaan (0.5-15) converged normally after 35 iterations
Number of observations 301
Estimator ML
Minimum Function Test Statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Model test baseline model:
Minimum Function Test Statistic 918.852
Degrees of freedom 36
P-value 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.896
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3737.745
Loglikelihood unrestricted model (H1) -3695.092
Number of free parameters 21
Akaike (AIC) 7517.490
Bayesian (BIC) 7595.339
Sample-size adjusted Bayesian (BIC) 7528.739
Root Mean Square Error of Approximation:
RMSEA 0.092
90 Percent Confidence Interval 0.071 0.114
P-value RMSEA <= 0.05 0.001
Standardized Root Mean Square Residual:
SRMR 0.065
Parameter estimates:
Information Expected
Standard Errors Standard
Estimate Std.err Z-value P(>|z|)
Latent variables:
visual =~
x1 1.000
x2 0.554 0.100 5.554 0.000
x3 0.729 0.109 6.685 0.000
textual =~
x4 1.000
x5 1.113 0.065 17.014 0.000
x6 0.926 0.055 16.703 0.000
speed =~
x7 1.000
x8 1.180 0.165 7.152 0.000
x9 1.082 0.151 7.155 0.000
Covariances:
visual ~~
textual 0.408 0.074 5.552 0.000
speed 0.262 0.056 4.660 0.000
textual ~~
speed 0.173 0.049 3.518 0.000
Variances:
x1 0.549 0.114
x2 1.134 0.102
x3 0.844 0.091
x4 0.371 0.048
x5 0.446 0.058
x6 0.356 0.043
x7 0.799 0.081
x8 0.488 0.074
x9 0.566 0.071
visual 0.809 0.145
textual 0.979 0.112
speed 0.384 0.086
>
library(semPlot)
semPaths(fit,
what="std",
edge.label.cex = 0.6,
sizeMan=5,
sizeLat=5,
curve=0.4
)
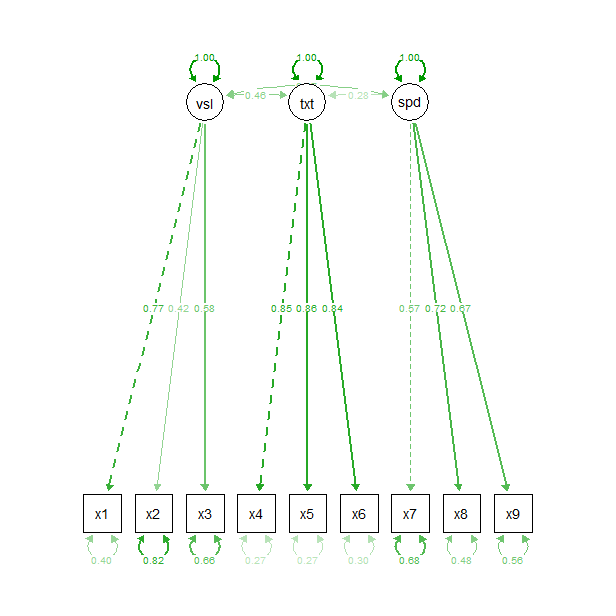
м•„лһҳмҷҖ к°ҷмқҙ н‘ңнҳ„н• мҲҳ мһҲмңјлӮҳ, м—Ҷм–ҙм§Ҳ н•ЁмҲҳлқјкі н•Ё.
library(qgraph)
qgraph.lavaan(fit, layout="tree", titles=F,
vsize.man=5,
vsize.lat=5,
filetype="",
include=4,
curve=-0.4,
edge.label.cex=0.6)
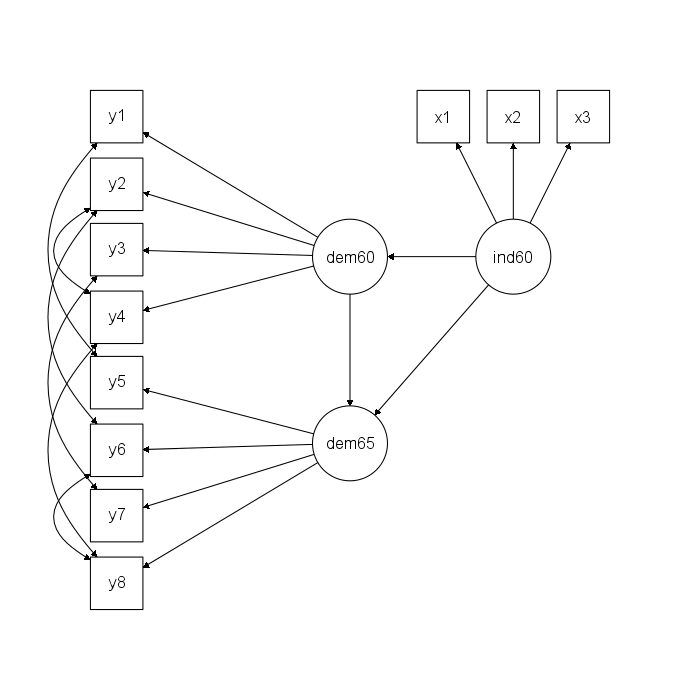
3 кө¬мЎ°л°©м •мӢқ(SEM, structural equation modeling) #
PoliticalDemocracy лҚ°мқҙн„°лҘј мӮ¬мҡ©н•ңлӢӨ.
PoliticalDemocracyм—җ лҢҖн•ң м„ӨлӘ…мқҖ
![[http]](/moniwiki/imgs/http.png) м—¬кё°(http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/lavaan/html/PoliticalDemocracy.html)
м—¬кё°(http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/lavaan/html/PoliticalDemocracy.html)лҘј м°ёкі н•ңлӢӨ.
library("lavaan")
data(PoliticalDemocracy)
model <- "
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
"
fit <- sem(model, data = PoliticalDemocracy)
summary(fit, standardized = TRUE)
> summary(fit, standardized = TRUE)
lavaan (0.5-15) converged normally after 68 iterations
Number of observations 75
Estimator ML
Minimum Function Test Statistic 38.125
Degrees of freedom 35
P-value (Chi-square) 0.329
Parameter estimates:
Information Expected
Standard Errors Standard
Estimate Std.err Z-value P(>|z|) Std.lv Std.all
Latent variables:
ind60 =~
x1 1.000 0.670 0.920
x2 2.180 0.139 15.742 0.000 1.460 0.973
x3 1.819 0.152 11.967 0.000 1.218 0.872
dem60 =~
y1 1.000 2.223 0.850
y2 1.257 0.182 6.889 0.000 2.794 0.717
y3 1.058 0.151 6.987 0.000 2.351 0.722
y4 1.265 0.145 8.722 0.000 2.812 0.846
dem65 =~
y5 1.000 2.103 0.808
y6 1.186 0.169 7.024 0.000 2.493 0.746
y7 1.280 0.160 8.002 0.000 2.691 0.824
y8 1.266 0.158 8.007 0.000 2.662 0.828
Regressions:
dem60 ~
ind60 1.483 0.399 3.715 0.000 0.447 0.447
dem65 ~
ind60 0.572 0.221 2.586 0.010 0.182 0.182
dem60 0.837 0.098 8.514 0.000 0.885 0.885
Covariances:
y1 ~~
y5 0.624 0.358 1.741 0.082 0.624 0.296
y2 ~~
y4 1.313 0.702 1.871 0.061 1.313 0.273
y6 2.153 0.734 2.934 0.003 2.153 0.356
y3 ~~
y7 0.795 0.608 1.308 0.191 0.795 0.191
y4 ~~
y8 0.348 0.442 0.787 0.431 0.348 0.109
y6 ~~
y8 1.356 0.568 2.386 0.017 1.356 0.338
Variances:
x1 0.082 0.019 0.082 0.154
x2 0.120 0.070 0.120 0.053
x3 0.467 0.090 0.467 0.239
y1 1.891 0.444 1.891 0.277
y2 7.373 1.374 7.373 0.486
y3 5.067 0.952 5.067 0.478
y4 3.148 0.739 3.148 0.285
y5 2.351 0.480 2.351 0.347
y6 4.954 0.914 4.954 0.443
y7 3.431 0.713 3.431 0.322
y8 3.254 0.695 3.254 0.315
ind60 0.448 0.087 1.000 1.000
dem60 3.956 0.921 0.800 0.800
dem65 0.172 0.215 0.039 0.039
>
library(semPlot)
semPaths(fit,
what="std",
edge.label.cex = 0.6,
sizeMan=5,
sizeLat=5,
curve=0.4,
edge.color="black"
)
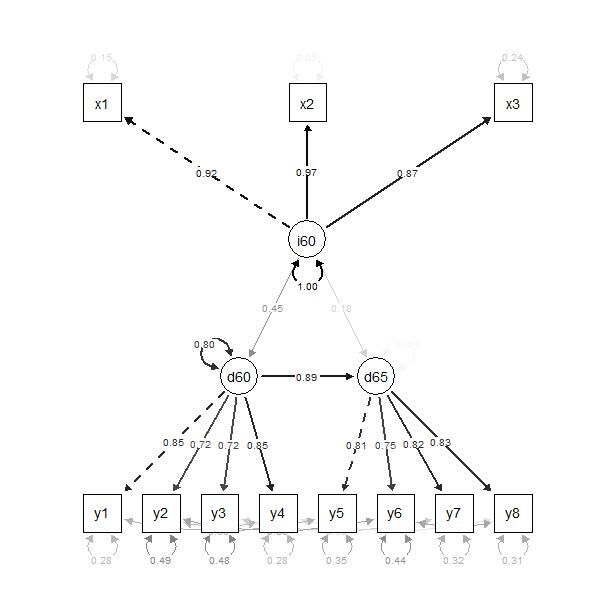
4.1 intercept #
model <- "
# three-factor model
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
# intercepts
x1 ~ 1
x2 ~ 1
x3 ~ 1
x4 ~ 1
x5 ~ 1
x6 ~ 1
x7 ~ 1
x8 ~ 1
x9 ~ 1
"
fit <- cfa(model, data = HolzingerSwineford1939, meanstructure=T)
summary(fit, fit.measures = TRUE)
library(semPlot)
semPaths(fit,
what="std",
edge.label.cex = 0.6,
sizeMan=5,
sizeLat=5,
curve=0.4,
edge.color="black"
)
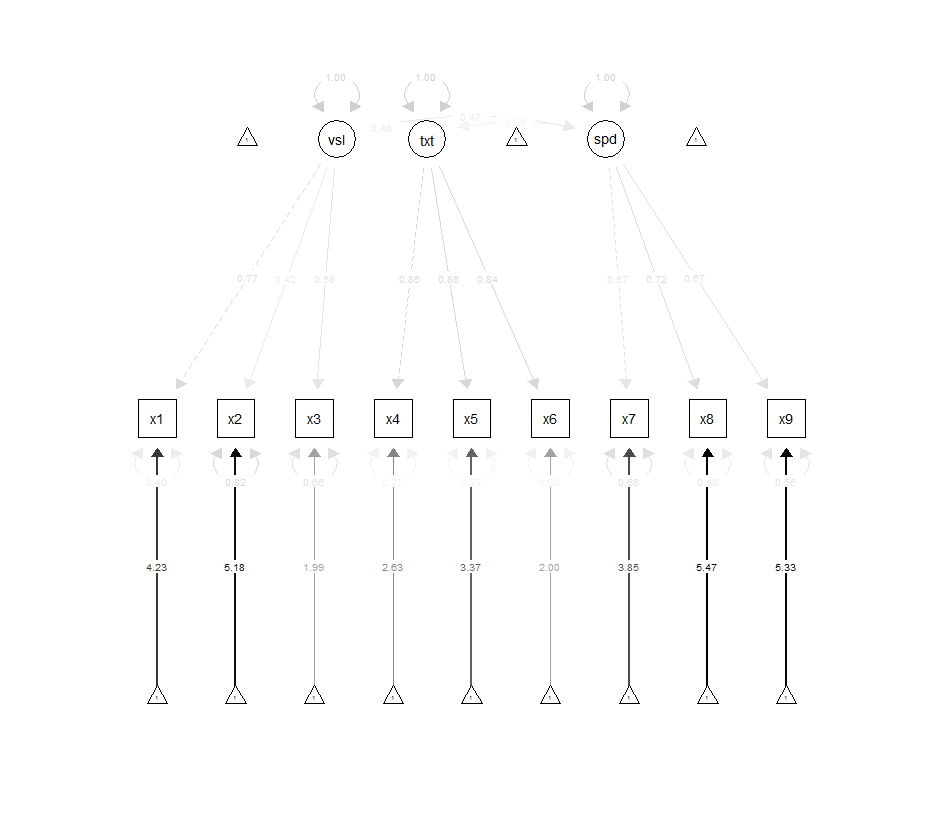
4.3 starting value #
model <- "
# three-factor model
visual =~ x1 + 0.5*x2 + c(0.6, 0.8)*x3
textual =~ x4 + start(c(1.2, 0.6))*x5 + a*x6
speed =~ x7 + x8 + x9
"
fit <- cfa(model, data = HolzingerSwineford1939, group="school")
summary(fit, fit.measures = TRUE)
starting valueк°Җ 0.5*x2к°ҷмқҙ мғҒмҲҳлЎң мЈјм–ҙ м§Ҳ мҲҳ мһҲлӢӨ. лҳҗн•ң c(0.6, 0.8)мҷҖ к°ҷмқҙ лІЎн„°лЎң groupлі„лЎң starting valueлҘј л”°лЎң мӨ„ мҲҳ мһҲлӢӨ.
4.4 fitting function #
HS.model <- ' visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9 '
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
group = "school",
group.equal = c("loadings"))
summary(fit)
group.equalм—җ loadings лҢҖмӢ лӢӨмқҢкіј к°ҷмқҖ кІғл“Өмқҙ мҳ¬ мҲҳ мһҲлӢӨ.
- intercepts: the intercepts of the observed variables
- means: the intercepts/means of the latent variables
- residuals: the residual variances of the observed variables
- residual.covariances: the residual covariances of the observed variables
- lv.variances: the (residual) variances of the latent variables
- lv.covariances: the (residual) covariances of the latent varibles
- regressions: all regression coefficients in the model
If you omit the group.equal argument, all parameters are freely estimated in each group (but the model structure is the same).
But what if you want to constrain a whole group of parameters (say all factor loadings and intercepts) across groups, except for one or two parameters that need to stay free in all groups. For this scenario, you can use the argument group.partial, containing the names of those parameters that need to remain free. For example:
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
group = "school",
group.equal = c("loadings", "intercepts"),
group.partial = c("visual=~x2", "x7~1"))
5 мҳҲм ң1 #
м°ёкі :
http://r-project.kr/content/r%EB%A1%9C-%ED%95%98%EB%8A%94-%EA%B5%AC%EC%A1%B0%EB%B0%A9%EC%A0%95%EC%8B%9D-lavaan2amos л¬ём„ңлҘј ліҙкі н•Ё.
library(lavaan)
> str(ch9.ex1)
'data.frame': 8 obs. of 5 variables:
$ attitude: int 2 3 3 4 4 4 4 5
$ loyalty : int 2 3 3 4 4 5 4 5
$ price : int 4 4 3 3 2 2 1 1
$ quality : int 2 3 2 3 3 4 3 5
$ design : int 2 3 4 2 5 3 2 4
> ch9.ex1
attitude loyalty price quality design
1 2 2 4 2 2
2 3 3 4 3 3
3 3 3 3 2 4
4 4 4 3 3 2
5 4 4 2 3 5
6 4 5 2 4 3
7 4 4 1 3 2
8 5 5 1 5 4
> path.model <- "
+ #regressions
+ attitude ~ price + quality + design
+ loyalty ~ attitude
+
+ #residual covariances
+ price ~~ quality
+ price ~~ design
+ quality ~~ design
+ "
> path.example <- lavaan(path.model, data=ch9.ex1, auto.var=T, auto.fix.first=T, fixed.x=F)
> summary(path.example)
lavaan (0.5-15) converged normally after 43 iterations
Number of observations 8
Estimator ML
Minimum Function Test Statistic 1.718
Degrees of freedom 3
P-value (Chi-square) 0.633
Parameter estimates:
Information Expected
Standard Errors Standard
Estimate Std.err Z-value P(>|z|)
Regressions:
attitude ~
price -0.382 0.133 -2.869 0.004
quality 0.459 0.159 2.883 0.004
design 0.063 0.109 0.579 0.562
loyalty ~
attitude 1.064 0.135 7.906 0.000
Covariances:
price ~~
quality -0.688 0.440 -1.563 0.118
design -0.313 0.431 -0.725 0.468
quality ~~
design 0.234 0.355 0.660 0.509
Variances:
attitude 0.097 0.048
loyalty 0.106 0.053
price 1.250 0.625
quality 0.859 0.430
design 1.109 0.555
> summary(path.example, fit.measures=T)
lavaan (0.5-15) converged normally after 43 iterations
Number of observations 8
Estimator ML
Minimum Function Test Statistic 1.718
Degrees of freedom 3
P-value (Chi-square) 0.633
Model test baseline model:
Minimum Function Test Statistic 40.609
Degrees of freedom 10
P-value 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.140
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -36.520
Loglikelihood unrestricted model (H1) -35.662
Number of free parameters 12
Akaike (AIC) 97.041
Bayesian (BIC) 97.994
Sample-size adjusted Bayesian (BIC) 62.535
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent Confidence Interval 0.000 0.481
P-value RMSEA <= 0.05 0.641
Standardized Root Mean Square Residual:
SRMR 0.021
Parameter estimates:
Information Expected
Standard Errors Standard
Estimate Std.err Z-value P(>|z|)
Regressions:
attitude ~
price -0.382 0.133 -2.869 0.004
quality 0.459 0.159 2.883 0.004
design 0.063 0.109 0.579 0.562
loyalty ~
attitude 1.064 0.135 7.906 0.000
Covariances:
price ~~
quality -0.688 0.440 -1.563 0.118
design -0.313 0.431 -0.725 0.468
quality ~~
design 0.234 0.355 0.660 0.509
Variances:
attitude 0.097 0.048
loyalty 0.106 0.053
price 1.250 0.625
quality 0.859 0.430
design 1.109 0.555
> summary(path.example, standardized=T)
lavaan (0.5-15) converged normally after 43 iterations
Number of observations 8
Estimator ML
Minimum Function Test Statistic 1.718
Degrees of freedom 3
P-value (Chi-square) 0.633
Parameter estimates:
Information Expected
Standard Errors Standard
Estimate Std.err Z-value P(>|z|) Std.lv Std.all
Regressions:
attitude ~
price -0.382 0.133 -2.869 0.004 -0.382 -0.498
quality 0.459 0.159 2.883 0.004 0.459 0.497
design 0.063 0.109 0.579 0.562 0.063 0.078
loyalty ~
attitude 1.064 0.135 7.906 0.000 1.064 0.942
Covariances:
price ~~
quality -0.688 0.440 -1.563 0.118 -0.688 -0.663
design -0.313 0.431 -0.725 0.468 -0.313 -0.265
quality ~~
design 0.234 0.355 0.660 0.509 0.234 0.240
Variances:
attitude 0.097 0.048 0.097 0.132
loyalty 0.106 0.053 0.106 0.113
price 1.250 0.625 1.250 1.000
quality 0.859 0.430 0.859 1.000
design 1.109 0.555 1.109 1.000
> library(qgraph)
Warning message:
нҢЁнӮӨм§Җ вҖҳqgraphвҖҷлҠ” R лІ„м „ 3.0.3м—җм„ң мһ‘м„ұлҗҳм—ҲмҠөлӢҲлӢӨ
> qgraph.lavaan(path.example, layout="spring",
+ vsize.man=8,
+ vsize.lat=8,
+ filetype="",
+ include=4,
+ curve=-0.4,
+ edge.label.cex=0.6)
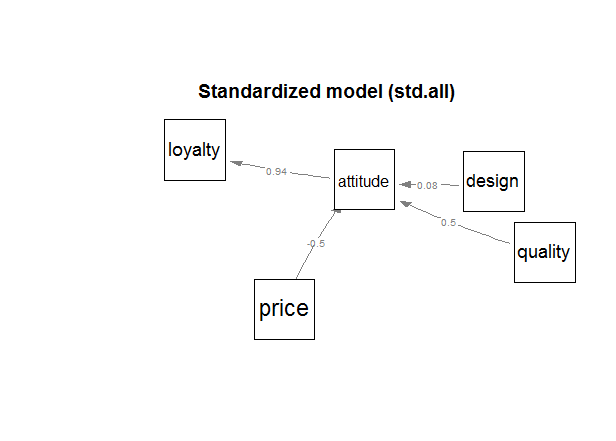
- лёҢлһңл“ңм—җ лҢҖн•ң нғңлҸ„(attitude)м—җ мҳҒн–Ҙмқ„ мЈјлҠ” мҡ”мқёмқҖ к°ҖкІ©(price), н’Ҳм§Ҳ(quality), мҷёнҳ•(design)мқёлҚ°,
- к°ҖкІ©мқҖ лӮ®мқ„ мҲҳлЎқ мўӢлӢӨ. (-0.5)
- н’Ҳм§ҲлҠ” мўӢмқ„ мҲҳлЎқ мўӢлӢӨ. (0.5)
- мҷёнҳ•мқҖ лі„лЎң кҙҖкі„к°Җ м—ҶлӢӨ. (0.08)
- 충м„ұлҸ„(royalty)лҠ” лёҢлһңл“ңм—җ лҢҖн•ң нғңлҸ„к°Җ мҳҒн–Ҙмқ„ мЈјлҠ” мҡ”мқёмқҙлӢӨ. (0.94)
6 мҳҲм ң2 #
http://www.inside-r.org/packages/cran/qgraph/docs/qgraph.lavaan
## Not run:
## The industrialization and Political Democracy Example
# Example from lavaan::sem help file:
require("lavaan")
## Bollen (1989), page 332
model <- '
# latent variable definitions
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + equal("dem60=~y2")*y6
+ equal("dem60=~y3")*y7
+ equal("dem60=~y4")*y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'
fit <- sem(model, data=PoliticalDemocracy)
# Plot standardized model (numerical):
qgraph.lavaan(fit,layout="tree",vsize.man=5,vsize.lat=10,
filetype="",include=4,curve=-0.4,edge.label.cex=0.6)
# Plot standardized model (graphical):
qgraph.lavaan(fit,layout="tree",vsize.man=5,vsize.lat=10,
filetype="",include=8,curve=-0.4,edge.label.cex=0.6)
# Create output document:
qgraph.lavaan(fit,layout="spring",vsize.man=5,vsize.lat=10,
filename="lavaan")
## End(Not run)
![[http]](/moniwiki/imgs/http.png) tutorial(http://lavaan.ugent.be/tutorial/index.html)мқ„ л”°лқјн•ҙ ліёкұ°лӢӨ. lavaanлҠ” "latent variable analysis(мһ мһ¬ ліҖмҲҳ 분м„қ)"мқҳ м•ҪмһҗлӢӨ. мһ мһ¬ ліҖмҲҳлһҖ, кҙҖмёЎ ліҖмҲҳлЎңл¶Җн„° м¶”м •лҗҳм–ҙ진 추мғҒм Ғ к°ңл…җмқҳ ліҖмҲҳлҘј л§җн•ңлӢӨ. кө¬мЎ° л°©м •мӢқмқҳ ліҖмҲҳл“Өм—җ лҢҖн•ң м„ӨлӘ…мқҖ
tutorial(http://lavaan.ugent.be/tutorial/index.html)мқ„ л”°лқјн•ҙ ліёкұ°лӢӨ. lavaanлҠ” "latent variable analysis(мһ мһ¬ ліҖмҲҳ 분м„қ)"мқҳ м•ҪмһҗлӢӨ. мһ мһ¬ ліҖмҲҳлһҖ, кҙҖмёЎ ліҖмҲҳлЎңл¶Җн„° м¶”м •лҗҳм–ҙ진 추мғҒм Ғ к°ңл…җмқҳ ліҖмҲҳлҘј л§җн•ңлӢӨ. кө¬мЎ° л°©м •мӢқмқҳ ліҖмҲҳл“Өм—җ лҢҖн•ң м„ӨлӘ…мқҖ ![[http]](/moniwiki/imgs/http.png) м—¬кё°(http://blog.naver.com/lucifer246?Redirect=Log&logNo=173521493)лҘј м°ёкі н•ҳмһҗ.
м—¬кё°(http://blog.naver.com/lucifer246?Redirect=Log&logNo=173521493)лҘј м°ёкі н•ҳмһҗ.




