[edit]
2 ks.test(мҪңлӘЁкі лЎңн”„-мҠӨлҜёлҘҙл…ён”„ кІҖм •) #
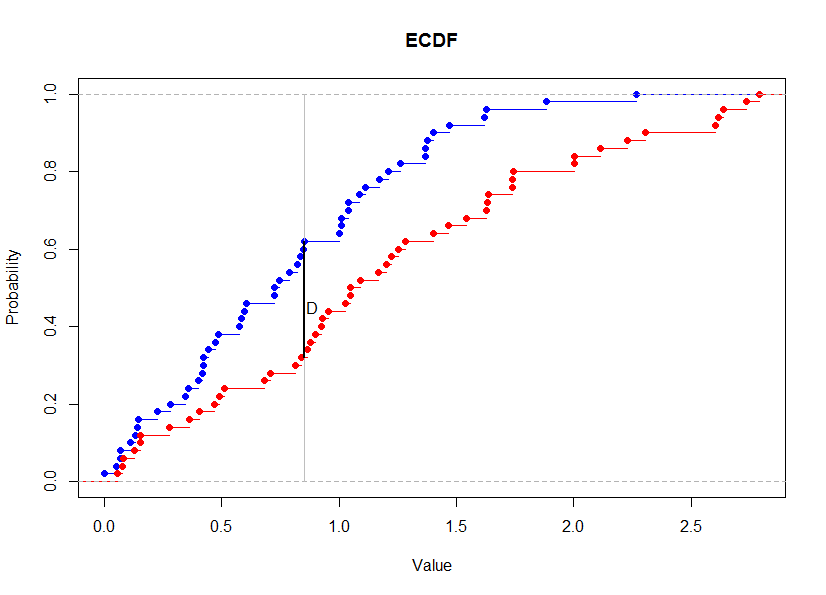
л‘җ ліҖмҲҳмқҳ ecdfмқҳ м°Ёмқҙк°Җ к°ҖмһҘ нҒ° к°’мңјлЎң мҪңлӘЁкі лЎңн”„-мҠӨлҜёлҘҙл…ён”„мқҳ кІҖм •нҶөкі„лҹүмқҳ м җ근분нҸ¬лҘј мқҙмҡ©н•ҳм—¬ кІҖм •н•ңлӢӨ.
x1 <- rnorm(50)
x2 <- rnorm(50, -1)
compare <- function(x, y) {
n <- length(x); m <- length(y)
w <- c(x, y)
o <- order(w)
z <- cumsum(ifelse(o <= n, m, -n))
i <- which.max(abs(z))
w[o[i]]
}
u <- compare(x1,x2)
e.x <- ecdf(x1)
e.y <- ecdf(x2)
abs(e.x(u) - e.y(u))
ks.test(x1,x2)$statistic
plot(e.x, col="Blue", main="ECDF", xlab="Value", ylab="Probability", xlim=range(c(x1,x2)))
plot(e.y, add=TRUE, col="Red")
lines(c(u,u), c(0,1), col="Gray")
lines(c(u,u), c(e.x(u), e.y(u)), lwd=2)
text(u*1.04, abs(e.x(u)-e.y(u)) * 1.5, label="D")

лҳҗ лӢӨлҘё л°©лІ•
x1 <- rnorm(50)
x2 <- rnorm(50, -1)
library("rgr")
gx.ks.test(x1, x2)
кІ°кіј
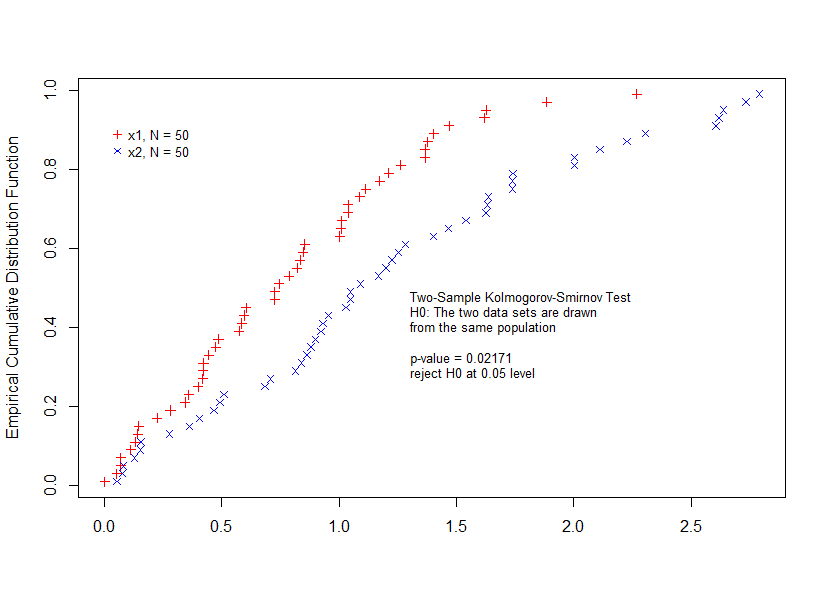
> gx.ks.test(x1, x2) Two-sample Kolmogorov-Smirnov test data: x1 and x2 D = 0.3, p-value = 0.02171 alternative hypothesis: two-sided

лҳҗ лӢӨлҘё л°©лІ•
plot(ecdf(x1), do.points = FALSE, verticals=T, xlim=range(x1, x2)) lines(ecdf(x2), lty=3, do.points = FALSE, verticals=T) ks.test(x1, x2, alternative="two.sided")