[edit]
5 n개의 집단 비율에 대한 검정 #
A도시에서는 300명 중 100명이, B도시에서는 400명 중 170명이 D후보를 지지한다고 조사되었다. A도시와 B도시의 D후부 지지 비율이 같다고 할 수 있는가?
분자 <- c(100, 170) 분모 <- c(300, 400) prop.test(분자, 분모)
> prop.test(분자, 분모) 2-sample test for equality of proportions with continuity correction data: 분자 out of 분모 X-squared = 5.6988, df = 1, p-value = 0.01698 alternative hypothesis: two.sided 95 percent confidence interval: -0.16664176 -0.01669158 sample estimates: prop 1 prop 2 0.3333333 0.4250000
결과해석
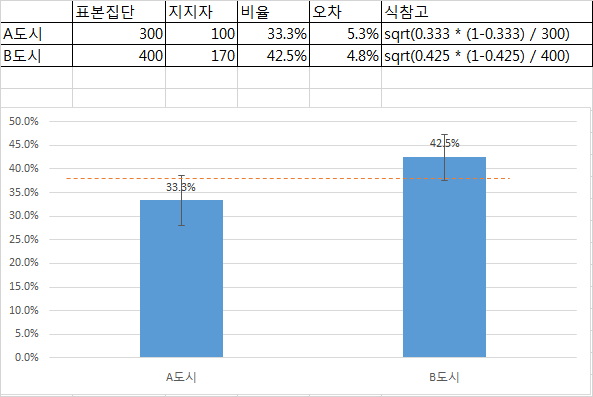
- 두 집단에서 어떤 사건에 대한 비율이 같다고 할 수 있는지에 대한 검정.
- 가설
- 귀무가설: 차이가 없다.
- 대립가설: 차이가 있다. --> 유의수준 0.05에서는 대립가설 지지, 유의수준 0.01에서는 대립가설 기각
- 귀무가설: 차이가 없다.
- 95% 신뢰구간: 0.4250000-0.16664176 ~ 0.4250000-0.01669158 = 0.2583582 ~ 0.4083084, 기준은 100/300
