[edit]
3 лӢӨлҘё л°©лІ• #
#install.packages("yacca")
library("yacca")
rs3 <- cca(d1, d2)
rs3
> rs3
Canonical Correlation Analysis
Canonical Correlations:
CV 1 CV 2
0.9558493 0.6976745
X Coefficients:
CV 1 CV 2
л””мһҗмқё -0.03428316 0.03920114
кё°лҠҘм„ұ -0.03030183 -0.05234068
Y Coefficients:
CV 1 CV 2
л§Өл ҘлҸ„ -0.02577813 -0.05651435
м„ нҳёлҸ„ -0.03411328 0.05890991
Structural Correlations (Loadings) - X Vars:
CV 1 CV 2
л””мһҗмқё -0.8654311 0.5010280
кё°лҠҘм„ұ -0.7527465 -0.6583105
Structural Correlations (Loadings) - Y Vars:
CV 1 CV 2
л§Өл ҘлҸ„ -0.8653783 -0.5011192
м„ нҳёлҸ„ -0.9098212 0.4150005
Aggregate Redundancy Coefficients (Total Variance Explained):
X | Y: 0.7675629
Y | X: 0.823285
> plot(rs3)
н•ҙм„қмқ„ н•ҙліҙл©ҙ...
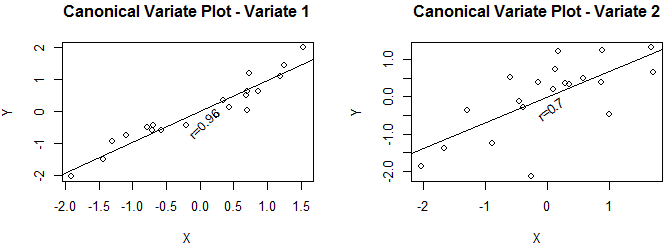

- м ң1м •мӨҖмғҒкҙҖліҖмҲҳ(CV1) - ліҖмҲҳк·ёлЈ№XмҷҖ ліҖмҲҳк·ёлЈ№YмҷҖмқҳ мөңлҢҖ мғҒкҙҖ кі„мҲҳлҠ” 0.96
- м ң2м •мӨҖмғҒкҙҖліҖмҲҳ(CV2) - ліҖмҲҳк·ёлЈ№XмҷҖ ліҖмҲҳк·ёлЈ№YмҷҖмқҳ мөңлҢҖ мғҒкҙҖ кі„мҲҳ лӢӨмқҢмңјлЎң лҶ’мқҖ мғҒкҙҖкі„мҲҳлҠ” 0.7
Canonical Correlations:
CV 1 CV 2
0.9558493 0.6976745
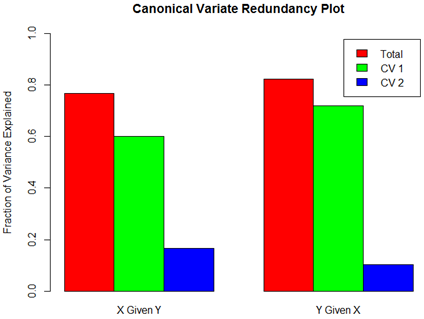
Aggregate Redundancy Coefficients (Total Variance Explained): X | Y: 0.7675629 Y | X: 0.823285
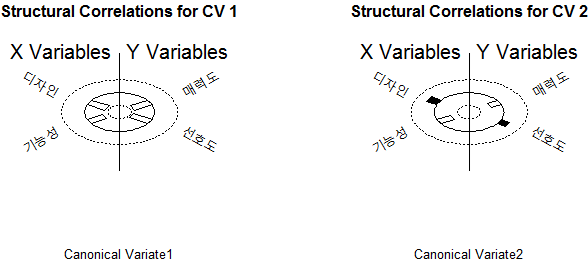
Structural Correlations (Loadings) - X Vars:
CV 1 CV 2
л””мһҗмқё -0.8654311 0.5010280
кё°лҠҘм„ұ -0.7527465 -0.6583105
Structural Correlations (Loadings) - Y Vars:
CV 1 CV 2
л§Өл ҘлҸ„ -0.8653783 -0.5011192
м„ нҳёлҸ„ -0.9098212 0.4150005
- м •мӨҖм Ғмһ¬(canonical loadings) - кІҖмҰқн•ҳлҠ” л°©лІ•
- Xк·ёлЈ№мқҳ ліҖмҲҳмқё л””мһҗмқё, кё°лҠҘм„ұкіј CV1, CV2мқҳ мғҒкҙҖкі„мҲҳ
- Yк·ёлЈ№мқҳ ліҖмҲҳмқё л§Өл ҘлҸ„, м„ нҳёлҸ„мҷҖ CV1, CV2мқҳ мғҒкҙҖкі„мҲҳ
- м°ёкі : м •мӨҖкөҗм°Ём Ғмһ¬(canonical cross-loadings, н•ң ліҖмҲҳмҷҖ н•ҙлӢ№ ліҖмҲҳк·ёлЈ№мқҙ м•„лӢҢ 비көҗк·ёлЈ№мқҳ м •мӨҖмғҒкҙҖліҖмҲҳмҷҖмқҳ мғҒкҙҖкҙҖкі„)лқјлҠ” кІғлҸ„ мһҲлӢӨ.
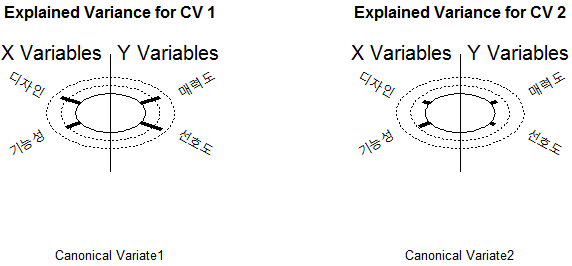
X Coefficients:
CV 1 CV 2
л””мһҗмқё -0.03428316 0.03920114
кё°лҠҘм„ұ -0.03030183 -0.05234068
Y Coefficients:
CV 1 CV 2
л§Өл ҘлҸ„ -0.02577813 -0.05651435
м„ нҳёлҸ„ -0.03411328 0.05890991
м •мӨҖмғҒкҙҖкі„мҲҳ
- CV1
- X = -0.03428316 * л””мһҗмқё + -0.03030183 + кё°лҠҘм„ұ
- Y = -0.02577813 * л§Өл ҘлҸ„ + -0.03411328 * м„ нҳёлҸ„
- X = -0.03428316 * л””мһҗмқё + -0.03030183 + кё°лҠҘм„ұ
- CV2
- X = 0.03920114 * л””мһҗмқё + -0.05234068 + кё°лҠҘм„ұ
- Y = -0.05651435 * л§Өл ҘлҸ„ + 0.05890991 * м„ нҳёлҸ„
- X = 0.03920114 * л””мһҗмқё + -0.05234068 + кё°лҠҘм„ұ
> X <- with(x, -0.03428316 * л””мһҗмқё + -0.03030183 * кё°лҠҘм„ұ)
> Y <- with(x, -0.02577813 * л§Өл ҘлҸ„ + -0.03411328 * м„ нҳёлҸ„)
> cor.test(X,Y)
Pearson's product-moment correlation
data: X and Y
t = 13.8003, df = 18, p-value = 5.156e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8896248 0.9827032
sample estimates:
cor
0.9558493
м–ҙлҠҗ м •мӨҖмғҒкҙҖкі„мҲҳк№Ңм§Җ м“ёлӘЁмһҲлӮҳ? (Bartlett's test)
> F.test.cca(rs3)
F Test for Canonical Correlations (Rao's F Approximation)
Corr F Num df Den df Pr(>F)
CV 1 0.95585 30.00045 4.00000 32 2.029e-10 ***
CV 2 0.69767 16.12224 1.00000 17 0.0008971 ***
---
Signif. codes: 0 вҖҳ***вҖҷ 0.001 вҖҳ**вҖҷ 0.01 вҖҳ*вҖҷ 0.05 вҖҳ.вҖҷ 0.1 вҖҳ вҖҷ 1
- м ң1м •мӨҖмғҒкҙҖліҖмҲҳ, м ң2м •мӨҖмғҒкҙҖліҖмҲҳ лӘЁл‘җ м“ёлӘЁмһҲлӢӨ.