[edit]
5 boxcox ліҖнҷҳ:нҡҢк·Җ분м„қ #
нҡҢк·Җ진лӢЁмңјлЎң мһ”м°Ём—җ лҢҖн•ң 분м„қмқ„ н•ҳлҠ”лҚ°, мһ”м°ЁлҠ”
- м •к·ң분нҸ¬лҘј л”°лқјм•јн•ҳкі , --> shapiro.test(resid(model))
- 분мӮ°мқҙ мқјм •н•ҳкі , --> bptest(model)
- нҠ№лі„н•ң 추세лҘј ліҙмқҙм§Җ м•Ҡм•„м•ј н•ңлӢӨ. --> dwtest(model)
лЁјм Җ ліҖмҲҳ ліҖнҷҳмқ„ н•ҳм§Җ м•ҠмқҖ мғҒнғңмҷҖ лЎңк·ёліҖнҷҳмқ„ н•ң мғҒнғңм—җм„ң нҡҢк·Җ분м„қмқ„ н•ҙліҙмһҗ.
- model <- lm(Volume~Height+Girth,data=trees)
- model <- lm(I(log(Volume))~Height+Girth,data=trees)
library("MASS")
boxcox(lm(Volume~Height+Girth,data=trees),lambda=seq(-1,1,by=.1))
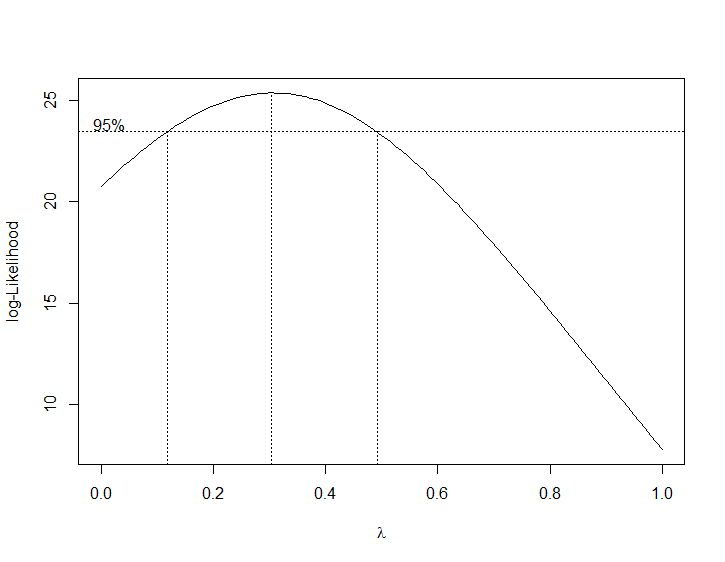
к·ёлҰјмқ„ ліҙл©ҙ м•ҢкІ м§Җл§Ң лҢҖлһө 0.3м—җм„ң lambdaк°Җ кІ°м •лҗңлӢӨлҠ” кІғмқ„ ліј мҲҳ мһҲлӢӨ. мөңм Ғмқҳ lambda к°’мқ„ м°ҫм•„ліҙмһҗ.
bc <- boxcox(lm(Volume~Height+Girth,data=trees),lambda=seq(-1,1,by=.1)) lambda <- bc$x[which.max(bc$y)]
кІ°кіј
> bc <- boxcox(lm(Volume~Height+Girth,data=trees),lambda=seq(-1,1,by=.1)) > lambda <- bc$x[which.max(bc$y)] > lambda [1] 0.3030303
lambda <- 0.3
model <- lm(I((Volume^lambda - 1)/lambda)~Height+Girth,data=trees)
shapiro.test(resid(model))
#install.packages("lmtest")
#library("lmtest")
bptest(model)
dwtest(model)
кІ°кіј
> shapiro.test(resid(model))
Shapiro-Wilk normality test
data: resid(model)
W = 0.96822, p-value = 0.4714
> library("lmtest")
н•„мҡ”н•ң нҢЁнӮӨм§ҖлҘј лЎңл”©мӨ‘мһ…лӢҲлӢӨ: zoo
лӢӨмқҢмқҳ нҢЁнӮӨм§ҖлҘј л¶Җм°©н•©лӢҲлӢӨ: вҖҳzooвҖҷ
The following objects are masked from вҖҳpackage:baseвҖҷ:
as.Date, as.Date.numeric
> dwtest(model)
Durbin-Watson test
data: model
DW = 2.069, p-value = 0.4811
alternative hypothesis: true autocorrelation is greater than 0
> dwtest(model)
Durbin-Watson test
data: model
DW = 2.069, p-value = 0.4811
alternative hypothesis: true autocorrelation is greater than 0
>
мһ”м°Ёмқҳ м •к·ңм„ұ, л“ұ분мӮ°м„ұ, лҸ…лҰҪм„ұмқ„ лӘЁл‘җ л§ҢмЎұн•ңлӢӨ.м°ёкі : ліҖмҲҳліҖнҷҳн•ң кІғмңјлЎң лӢӨмӢң мӣҗлһҳлҢҖлЎң..
b <- 100 lambda <- 0.2 y <- (b^lambda - 1)/lambda ((y*lambda) + 1)^(1/lambda)