install.packages("car")
library("car")
plot(population ~ year, data=USPop, main="(a)")
abline(lm(population ~ year, data=USPop))
xx <- USPop$year fit <- lm(population ~ poly(year, 2), data=USPop) lines(xx, predict(fit, data.frame(year=xx)), col="purple")
curve(1/(1+exp(-(-1 + 1*x))), from=-5, to=5, main="(b)") abline(h=1/2, lty=2) abline(v=1, lty=2)
fit <- nls(population ~ SSlogis(year, Asym, xmid, scal), data=USPop) summary(fit) xx <- USPop$year plot(population ~ year, data=USPop, main="(a)") lines(xx, predict(fit, data.frame(year=xx)), col="purple")
SSasymp(input, Asym, R0, lrc) SSasympOff(input, Asym, lrc, c0) SSasympOrig(input, Asym, lrc) SSbiexp(input, A1, lrc1, A2, lrc2) SSfol(Dose, input, lKe, lKa, lCl) SSfpl(input, A, B, xmid, scal) SSgompertz(input, Asym, b2, b3) SSlogis(input, Asym, xmid, scal) SSmicmen(input, Vm, K) SSweibull(input, Asym, Drop, lrc, pwr)
xx <- USPop$year plot(population ~ year, data=USPop, main="(a)") fit1 <- nls(population ~ SSlogis(year, Asym, xmid, scal), data=USPop) lines(xx, predict(fit1, data.frame(year=xx)), col="purple") fit2 <- nls(population ~ SSweibull(year, Asym, Drop, lrc, pwr), data=USPop) lines(xx, predict(fit2, data.frame(year=xx)), col="red") fit3 <- nls(population ~ SSfpl(year, A, B, xmid, scal), data=USPop) lines(xx, predict(fit3, data.frame(year=xx)), col="green")
Functions in base R stats package SSasymp (Asymptotic) SSasympOff (Asymptotic with an offset) SSasympOrig (Asymptotic through the Origin) SSbiexp (Bi-exponential) SSfol (First order compartment) SSfpl (Four parameter logistic) SSgompertz (Gompertz) SSlogis (Logistic) SSmicmen (Michaelis-Menten) SSweibull (Weibull) Functions in this package (nlraa) SSbgf (Beta-Growth Function) SSbgf4 (Four Parameter Beta-Growth Function) SSbgrp (Beta-Growth Reparameterized) SSbg4rp (Four Parameter Beta-Growth Reparameterized) SSdlf (Declining Logistic Function) SSricker (Ricker population growth) SSprofd (Profile of protein distribution) SSnrh (Non-rectangular hyperbola) SSlinp (linear-plateau) SSplin (plateau-linear) SSquadp (quadratic-plateau) SSpquad (plateau-quadratic) SSblin (bilinear) SSexpf (exponential function) SSexpfp (exponential-plateau) SSpexpf (plateau-exponential) SSbell (bell-shaped function) SSratio (rational function) SSlogis5 (five-parameter logistic) SStrlin (tri-linear function) SSexplin (expolinear)
install.packages("chemCal")
library("chemCal")
fit1 <- rlm(dau ~ x, data=tmp)
inverse.predict(fit1, 500000) #dau螳 500000 る x 覈伎伎 螳?
> head(df) seq u 1 1 4311 2 2 2381 3 3 1981 4 4 1529 5 5 1386 6 6 1340
x1 <- df[1:7,]
x2 <- df[8:nrow(df),]
cc1 <- coef(lm(log(u) ~ seq, data=x1))
cc2 <- coef(lm(log(u) ~ seq, data=x2))
fit <- nlsLM(u ~ a*exp(b * seq) + c * exp(d * seq),
start = list(a=cc1[1], b=cc1[2], c=cc2[1], d=cc2[2]),
data=df)
#exp * 3
r <- sort(unique(df.ko$ranking))
xlim <- c(1,max(r))
ylim <- c(0, max(df.ko$amt) + max(df.ko$amt) * 0.3)
plot(df.ko$ranking, df.ko$amt, cex=0.1, pch=19, xlim=xlim, ylim=ylim, xlab="谿", ylab="u", main="bi-exp")
x1 <- df.ko[df.ko$ranking <= 7,]
x2 <- df.ko[df.ko$ranking > 7 & df.ko$ranking <= 20 ,]
x3 <- df.ko[df.ko$ranking > 21,]
cc1 <- coef(lm(log(amt) ~ ranking, data=x1))
cc2 <- coef(lm(log(amt) ~ ranking, data=x2))
cc3 <- coef(lm(log(amt) ~ ranking, data=x3))
fit <- nlsLM(u ~ a*exp(b * seq) + c*exp(d * seq) + e*exp(f * seq),
start = list(a=cc1[1], b=cc1[2], c=cc2[1], d=cc2[2], e=cc3[1], f=cc3[2]),
data=df)
summary(fit)
lines(r, predict(fit, data.frame(ranking=r)), col="red")
#text(df$seq, df$u, df$w, cex=0.5, pos=4)
amt1 <- predict(fit, data.frame(ranking=r))
amt1 / sum(amt1)
r <- sort(unique(df.ko$ranking))
xlim <- c(1,max(r))
ylim <- c(0, max(df.ko$amt) + max(df.ko$amt) * 0.3)
plot(df.ko$ranking, df.ko$amt, cex=0.1, pch=19, xlim=xlim, ylim=ylim, xlab="", ylab="襷れ", main="蟲")
lines(r, predict(fit, data.frame(ranking=r)), col="red")
lines(r, coef(fit)[1]*exp(coef(fit)[2] * df$seq), col="blue")
lines(r, coef(fit)[3]*exp(coef(fit)[4] * df$seq), col="green")
lines(r, coef(fit)[5]*exp(coef(fit)[6] * df$seq), col="black")
fun <- function(x, mu, sd){
a <- 1/(x * sqrt(2*pi*sd))
b <- (log(x)-mu)^2 * -1
c <- 2 * sd^2
return (a * exp(b/c))
}
#data
val <- c(462604.2114,724545.9975,677961.1773,556621.1925,572068.4823,550408.0245,442748.9577,463050.285,485241.4509,406399.9335,394768.1661,474606.3792,408121.4988,254290.8273,234755.1933,201690.9834,
175243.2,171106.0665,228024.2613,199481.5251,141505.8969,148199.988,138756.7692,140078.0631,146512.2765,183688.7274,169084.7955,103705.1421,107350.3998,106554.8355,99301.161,105367.9611,148672.9455,
135343.5096,73087.3671,75604.4967,69973.8132,66367.3878,72191.2371,98143.1619,88506.7773,59722.086,59705.1591,54111.3165,49504.2126,50762.7774,68940.2766,67763.3592,50401.3383,50509.8696,51749.5161,
56774.814,56875.3797,65898.4131,58036.3659,45687.6945,44862.2592,41548.5696,37896.342,39405.8232,54220.8435,50035.9164,36221.5746,35067.5583,33099.0594,41550.561,33312.1392,42200.7531,36982.2894,26394.0156,
25939.9764,24163.6476,23641.9008,25495.8942,35859.1398,31292.8596,20783.2461,21233.3025,20770.302,20744.4138,19822.3956,31262.9886,28102.6368,17650.7739,17666.7051,17097.1647,16079.5593,17644.7997,26329.2951,
22879.1946,14800.0848,15000.2205,15227.2401,19307.6187,20345.1381,27219.4509,22791.573,14828.9601,26459.7318,65060.0337)
seq <- 1:length(val)
tmp <- data.frame(seq, val)
#log-normal function
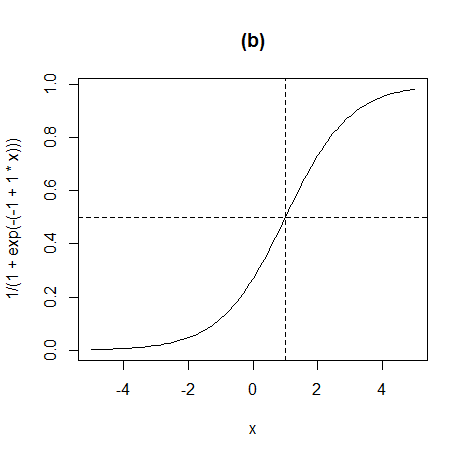
fun <- function(x, mu, sd){
a <- 1/(x * sqrt(2*pi*sd))
b <- (log(x)-mu)^2 * -1
c <- 2 * sd^2
return (a * exp(b/c))
}
#fitting
library("minpack.lm")
fit <- nlsLM(val ~ a * fun(seq, b, c) + d,
start = list(a=1, b=0.01, c=100, d=1),
control = nls.lm.control(maxiter = 1000),
trace = TRUE,
data=tmp)
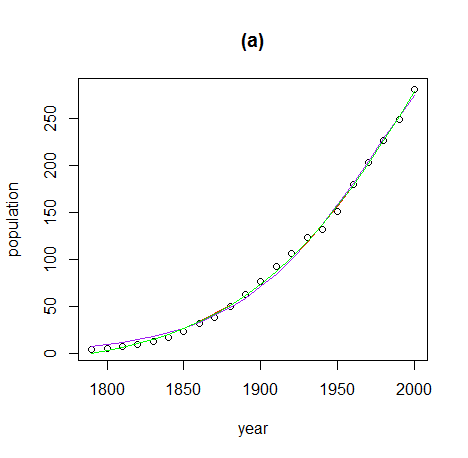
#plotting
r <- sort(unique(tmp$seq))
xlim <- c(1,max(r))
ylim <- c(0, max(tmp$val) + max(tmp$val) * 0.3)
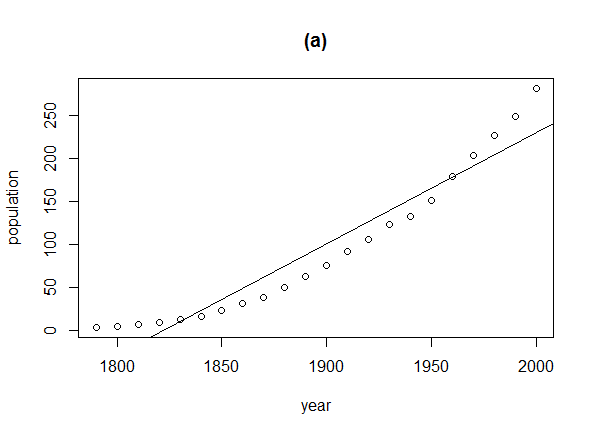
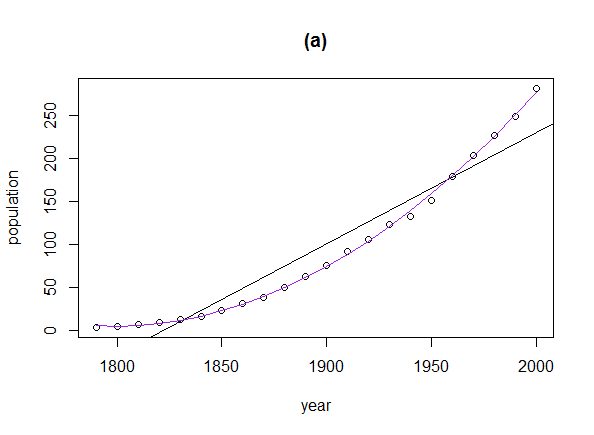
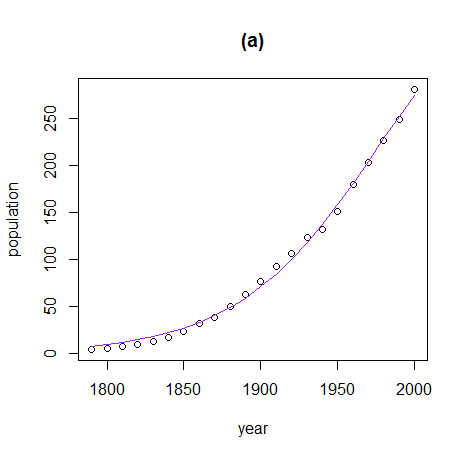
plot(tmp$seq, tmp$val, cex=0.1, pch=19, xlim=xlim, ylim=ylim)
lines(r, predict(fit, data.frame(seq=r)), col="red")
pareto <- function(y, m, s) {
return (s * (1 + y/(m * (s-1)))^(-s-1)/(m * (s-1)))
}
install.packages("rmutil")
library("rmutil")
dpareto(y, m, s, log=FALSE)
ppareto(q, m, s)
qpareto(p, m, s)
hpareto(y, m, s)
rpareto(n, m, s)
library("minpack.lm")
fit <- nlsLM(u ~ a*seq^b + c*seq^d + e*seq^f,
start = list(a=40000000, b=-0.05, c=8015503, d=-0.05, e=1674444, f=-0.05),
control = nls.lm.control(maxiter=1000),
data=df, trace=T)
summary(fit)
calcPeriod <- function(x, y){
incr <- x[2] - x[1]
tmp <- spectrum(y, plot=FALSE)
p <- (1/tmp$freq*incr)[which.max(tmp$spec)] # max of spectrum
p
}
x <- seq(0, 50, by = 0.05)
y <- sin(x)
p <- calcPeriod(x, y) # result = 2pi
tmp <- textConnection(
"prop seq
0.12 1
0.13 2
0.09 3
0.05 4
0.04 5
0.04 6
0.03 7
0.02 8
0.02 9
0.03 10
0.01 11
0.01 12
0.02 13
0.05 14
0.03 15
0.02 16
0.02 17
0.02 18
0.02 19
0.03 20
0.08 21")
mydata <- read.table(tmp, header=TRUE)
close.connection(tmp)
head(mydata)
mydata$x <- mydata$seq / (nrow(mydata)+1)
barplot(mydata$prop, names.arg=mydata$grp)
#x<-seq(0.01, 0.99, 0.01)
#barplot(dbeta(x, 0.1, 0.4))
#install.packages("minpack.lm")
library("minpack.lm")
fit <- nlsLM(prop ~ dbeta(x, a, b) * c, start = list(a=0.1, b=0.4, c=0.1), data=mydata, trace=T)
summary(fit)
plot(mydata$x, mydata$prop, type="h", lwd = 10, col="lightGrey", ylim=c(0, 0.2))
lines(mydata$x,fitted(fit))
set.seed(3) x <- rgamma(1e5, 2, .2) plot(density(x)) # normalize the gamma so it's between 0 & 1 # .0001 added because having exactly 1 causes fail xt <- x / ( max( x ) + .0001 ) # fit a beta distribution to xt library( MASS ) fit.beta <- fitdistr( xt, "beta", start = list( shape1=2, shape2=5 ) ) x.beta <- rbeta(1e5,fit.beta$estimate[[1]],fit.beta$estimate[[2]]) ## plot the pdfs on top of each other plot(density(xt)) lines(density(x.beta), col="red" ) ## plot the qqplots qqplot(xt, x.beta)
plot(df$x,df$y,xlim=c(0,0.7),pch=20) xnew <- seq(par()$usr[1],par()$usr[2],0.01) RegLine <- predict(m0,newdata = data.frame(x=xnew)) lines(xnew,RegLine,lwd=2) lines(xnew,RegLine+summary(m0)$sigma*1.96,lwd=2,lty=3) lines(xnew,RegLine-summary(m0)$sigma*196,lwd=2,lty=3)--豢豌: https://stackoverflow.com/questions/32459480/r-confidence-bands-for-exponential-model-nls-in-basic-graphics
test <- data.frame(times=c(0,5,10,15,30,50,60,90,120,180,240), RNA=c(0.48, 1.15, 1.03, 1.37, 5.55, 16.77, 20.97, 21.67, 10.50, 2.28, 1.58))
nonlin <- function(t, a, b, c) { a * (exp(-(abs(t-c) / b))) }
nlsfit <- nls(RNA ~ nonlin(times, a, b, c), data=test, start=list(a=25, b=20, c=75))
with(test, plot(times, RNA, pch=19, ylim=c(0,40)))
tseq <- seq(0,250,.1)
pars <- coef(nlsfit)
print(pars)
lines(tseq, nonlin(tseq, pars[1], pars[2], pars[3]), col=2)
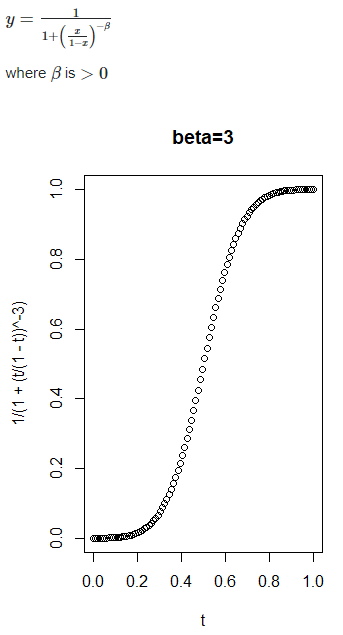
Appendix-Nonlinear-Regression.pdf ![[http]](/moniwiki/imgs/http.png)
豢豌(http://socserv.mcmaster.ca/jfox/Books/Companion/appendix/Appendix-Nonlinear-Regression.pdf)